Why is an accurate global map hard to make?

[Trekker4747]

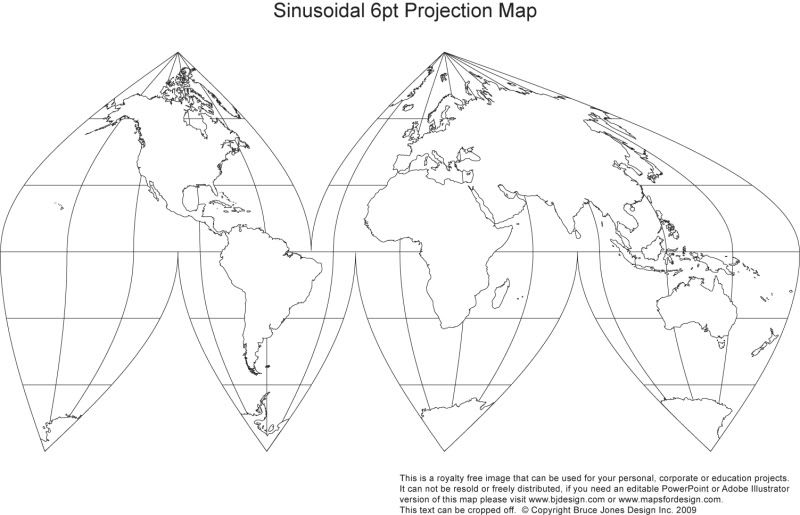
Maps of the world are often criticized for being inaccurate to the true sizes of the various continents. First there's the fairly standard one which makes Greenland is large as pretty much all of North America and Alaska the size of the entire mid-west then there's another version the smooshes the higher latitudes and lower latitudes while "normalizing" the more central ones.

I understand you're trying to take something that's on a spheroid surface and trying to represent it onto a flat diagram but is it really so hard to do without jacking up the size of things?

From our piddly little perspectives the Earth is pretty much "flat" to begin with. So why can't a flat, plain, map of the globe be made that accurately shows the sizes of all of the continents without having to alter them and without the "flattened" map be a crazy looking jumble and rather be rectangular. The rule with which you'd have to use measure distances would probably have to pretty non-intuitive, sure, but it can't be that hard to take something that is 24,000 miles round and condense it into a flat, straight, surface that's a foot or so across (depending on the size of map you want.)

 

[RoJoHen]

If you use the equator as the middle of the map, then the poles would inevitably have to get stretched out if you insist on the map being a rectangle. You could probably keep the continents more or less the correct size, but then you'd have to stretch out the oceans in between to compensate.

I mean, you can't take a rectangular piece of paper and roll it into a sphere, can you?

 

[Trekker4747]

If you use the equator as the middle of the map, then the poles would inevitably have to get stretched out if you insist on the map being a rectangle. You could probably keep the continents more or less the correct size, but then you'd have to stretch out the oceans in between to compensate.

I mean, you can't take a rectangular piece of paper and roll it into a sphere, can you?

If I had a piece of paper the size of the earth I'm pretty sure I could make a damn good spheroid shape, granted there'd be some cutting and splicing and bit of overlap involved...

 

[RoJoHen]

Okay...then I guess I don't see what you're trying to say. We can't just unroll the Earth and turn it into a rectangle. That's not how shapes work. Any map of the Earth is going to either have to be distorted or cut apart.

 

[thestrangequark]

^Yeah, I don't really get the confusion either.

 

[Trekker4747]

I think a better balance can be found without distorting the continents way out of proportion.

 

[RoJoHen]

Well, if you can figure it out, go for it. I have a feeling expert mapmakers would have done it already if it were possible.

 

[Finn]

I think a better balance can be found without distorting the continents way out of proportion.

Cutting and disorting is the "balance" you speak of...

Have you ever tried to flatten one entire piece of orange peel?

 

[thestrangequark]

I think a better balance can be found without distorting the continents way out of proportion.

Like this?

 

[David cgc]

If I had a piece of paper the size of the earth I'm pretty sure I could make a damn good spheroid shape, granted there'd be some cutting and splicing and bit of overlap involved...

Now we run into the wonderful world of map projections. I remember when I was in grade school, one of the geography textbooks had a little primer with examples and the various trade-offs of all the projections. Let me see if I can find something like it...

Wikipedia has a very comprehensive article, but it's not quite as accessible as the primer I was thinking of.

The first example they gave was if you wanted to flatten out an orange rind on a table, it would split itself into wedges, looking like this.

And it appears that your dream most closely aligns to the Gall-Peters projection, specifically designed to compensate for the inflation of size that occurs near the pole in the Mercator projection.

 

[RoJoHen]

I think a better balance can be found without distorting the continents way out of proportion.

Like this?

But you murdered Antarctica!

 

[Trekker4747]

And it appears that your dream most closely aligns to the Gall-Peters projection, specifically designed to compensate for the inflation of size that occurs near the pole in the Mercator projection.

Yeah, that's... close but at the same time Greenland gets all weird and flat and northeast North America gets enlongated a bit, as well as Northern Canada getting flattened a bit.

I'm looking at a globe now and, believe me, I understand the difficulty, inherent, in pulling something like this off but most of the flat-maps I've seen on first glance can give one an odd impression of the sizes and shapes of the continents.

 

[iguana_tonante]

I understand you're trying to take something that's on a spheroid surface and trying to represent it onto a flat diagram but is it really so hard to do without jacking up the size of things?

It's not just that's difficult. It's impossible.

You simply can't represent a sphere on a plane without some kind of distortion. You can choose what distortion you can have (angles, areas, etc), but you can't have you pie and eat it. Mapmakers suspected it since they realized the Earth was a sphere (around 3rd century BC), but I think it was Carl Gauss who proved it during the early 19th century.

Personally, I like the Mollweide projection. Looks like a good compromise.

 

[Miss Chicken]

I first heard of the Peters Projection map when I saw this clip

[yt]http://www.youtube.com/watch?v=n8zBC2dvERM[/yt]

 

[Trekker4747]

If Dr. Phlox is for it I am!

 

[Lord Garth]

I think a better balance can be found without distorting the continents way out of proportion.

Like this?

This is the type of global map I favor. Greenland shouldn't look so large.

 

[ShamelessMcBundy]

This reminds me of an Onion article. Greenland Thinks It Looks Fat In Mercator Map.

 

[scotpens]

. . . it appears that your dream most closely aligns to the Gall-Peters projection, specifically designed to compensate for the inflation of size that occurs near the pole in the Mercator projection.

Reading that Wiki piece, I was amused by the accounts of infighting within the cartographic community and the politicization of mapmaking. I mean, really — “cartographic imperialism”? The Mercator projection was designed for navigation, and its only real advantage is that it makes it easy to plot courses by sea.

 

[Canadave]

Yeah, as others have said, it's essentially impossible to translate a sphere onto a flat plane without distorting something. The classic dilemma of map projections is that no matter what you do, you're going to have to distort something, as no map of the world can accurately show all three of distance, direction, and size. The Mercator Projection, for example, is actually very, very good at displaying direction, which is why it became so popular. When you're a navigator at sea, being able to accurately plot what direction you need to go to to get to your destination is rather important, so you take along maps in Mercator.

Sinusoidal, though, demonstrates what happens when you try and fix the problems of distance and size. Though size becomes very accurate, direction and distance are distorted significantly. Or you've got the Azimuthal Equidistant Projection, which obviously displays accurate distance, while distorting size and direction way out of proportion.

Finally, you've got the compromises, like the Robinson Projection, which distorts all three aspects of the map, but does so without straying too far from a reasonable degree of accuracy:

So, Antarctica is too big, but not wildly out of proportion, and you may not be able to navigate with it, but you can head in vaguely the right direction, at least.

In short, map projections are big, complicated deal when it comes to cartography, and the only real solution is to chose the projection that best suits the map you're working on. Need to map the United States? Use the North American Datum, which is optimized for the USA and southern Canada. Need to see how far apart Australia and Brazil are? Azimuthal Equidistant. It's a pain, but when you're trying to model a sphere (which the Earth, technically speaking, isn't) on a flat plane, you just have to chose what you want to sacrifice, essentially.

 

[Itisnotlogical]

It's because the Earth is a sphere, and paper is flat. Because a sphere has no corners, it can't accurately be "unfolded" and portrayed, in its entirety, on a piece of paper.